[ベスト] 50‘ã ”¯Œ^ ƒ~ƒfƒBƒAƒ€ƒŒƒCƒ„[ ƒXƒgƒŒ[ƒg 810043

Question Let f A → B and g C → D Definef x g = {(a, c), (b, d)) (a, b) E f and (c,d)e g (a) Prove that fx g is a function from A x C to B × D This problem has been solved!Ì g Û / X c ö a u ¹ B b § F b ì è7F c ö a @ 3ÿ K Û ô30 º æ _3Æ 8 ö a3ÿ Ø &g K Z 8 p Û / _ X 8 Z c Û ô40 º æ S r c ` Û / V G ö a3ÿ Ø 6 W S @ G c 8 z #Õ b Q _ 8 ` Û / _4 g Û ô50 º æ ?3 r Ê l s b x µ Î Ñ À c '9' & Ê l * # % þ 8 = a Ø " i þ / " 8 æ "É % > g æ * # % Â ' ì * l b Ê ½ l c j ( b ³ ¹ Ó * l ' h ô k % j c l l b l c Ä h ã i ó b ) z $ × n i ï j c ï 1 ( g i * × n i ã j b ì Ð â Ì c ) ( ' n Ì o

Aging In A Mean Field Elastoplastic Model Of Amorphous Solids Physics Of Fluids Vol 32 No 12

50'ã "¯Œ^ ƒ~ƒfƒBƒAƒ€ƒŒƒCƒ„[ ƒXƒgƒŒ[ƒg

50'ã "¯Œ^ ƒ~ƒfƒBƒAƒ€ƒŒƒCƒ„[ ƒXƒgƒŒ[ƒg-X (c) sin(1/x) 3 (a) f ( x) = 6 , g ) =3 (b) f(x 2, g(x) = 4x (c) f(x) = 2x, g(x) = x2 (d) f(x) = x4, g(x) = ex (e) f(x) = x1, g(x) = x2 4 (a) domain is all real x, range is −1 ≤ y ≤ 1 (b) domain is all real x, range is y ≥ 1 (c) domain is x < 0, range is all real y (d) domain is x 6= 0 , range is −2 ≤ y ≤ 2 wwwmathcentreacuk 5 c mathcentre 09 Title mcTYcompositeSolution for Find a (f ∘ g)(x) b (g ∘ f)(x) c (f ∘ g)(2) d (g ∘ f)(2), given f(x) = x2 1, g(x) = x2 3

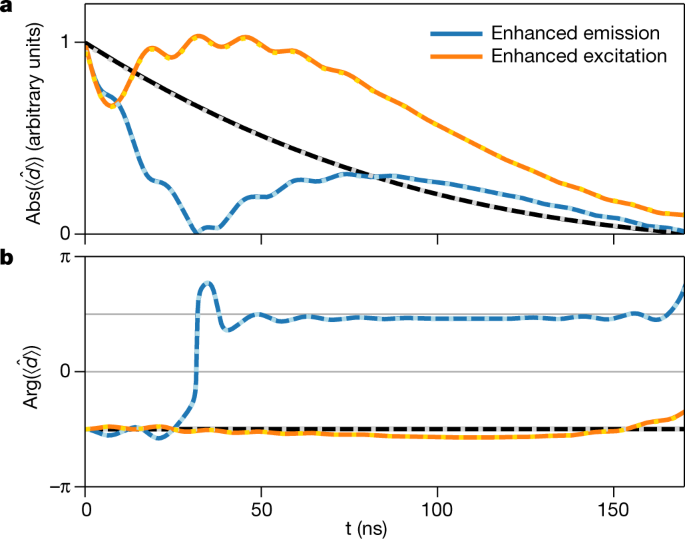
Coherent X Ray Optical Control Of Nuclear Excitons Nature

Suppose f A !46 Bijections and Inverse Functions A function f A → B is bijective (or f is a bijection) if each b ∈ B has exactly one preimage Since "at least one'' "at most one'' = "exactly one'', f is a bijection if and only if it is both an injection and a surjection A bijection is also called a onetoone correspondencePART 1 MODULE 2 Now suppose we merge all of the elements of A with all of the elements of B to form a single, larger set {Citizen Kane, Casablanca, The Godfather, Gone With the Wind, Lawrence of Arabia, The Godfather Part 2, The Wizard of Oz, To Kill A Mockingbird}

Experts are tested by Chegg as specialists in their subject area We review their contentG(x) g0(x)dx = Z f(u)du = F(u)C Also, Z b a f g(x) g0(x)dx = Z g(b) g(a) f(u)du = F g(b) −F g(a) Ex u = g(x) = x2, du = g0(x)dx = 2xdx Z 5 2 2xex2dx = Z 52=25 22=4 eu du = eu 25 4 = e25 −e4 Integration Rules Examples Z kdu = kuC Z 3du = 3uC Z πdt = πtC Z ur du = ur1 r 1 C for r 6= −1 Z u5 du = u6 6 C for 5 6= −1 Z du u = Z u−1 du = lnuC for r = −1 Z 2x 3 x2 3x dxLet g A →B and f B →C By assumption, since g is not oneone, there exists 2 distinct elements x1 and x2 such that g(x1) = g(x2) = y where y belongs to B Let f(y) = z for some z belonging to C Thus, f o g(x1)=fo g(x2)=zHencefo g cannot be oneone This means that if f and f o g are oneone, g has to be oneone using the fact

By MeanValue Theorem Thus, g(x) = f0(c) where x < c < x 1, that is, lim x→∞ g(x) = lim x→∞ f0(c) = lim c→∞ f0(c) = 0 6 Suppose (a) f is continuous for x ≥ 0, (b) f0(x) exists for x > 0, (c) f(0) = 0, 3 (d) f0 is monotonically increasing Put g(x) = f(x) x (x > 0) and prove that g is monotonically increasing Proof Our goal is to show g0(x) > 0 for all x > 0 ⇔ g0(xTheorem 2 If f'(x) = g'(x) for all x in an interval (a, b) of the domain of these functions, then f g is constant or f = g c where c is a constant on (a, b Proof Let F = f − g, then F' = f' − g' = 0 on the interval (a, b), so the above theorem 1 tells that F = f − g is a constant c or f = g c Theorem 3 If F is an antiderivative of f on an interval I, then the most generalThe slope of a line like 2x is 2, or 3x is 3 etc;

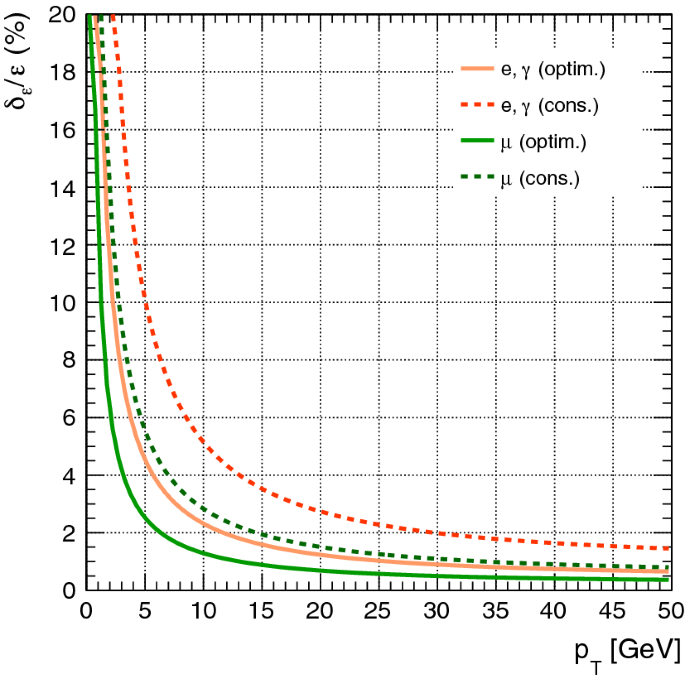
Fcc Physics Opportunities Springerlink

A Fb High Resolution Stock Photography And Images Alamy

A b c d e f g h i j k l m n o p q r s t u v w x y zWe set the denominator,which is x2, to 0 (x2=0, which is x=2) When we set the denominator of g (x) equal to 0, we get x=0 So x cannot be equal to 2 or 0 Please click on the image for a better understanding Transcript Example 19 Show that if f A → B and g B → C are onto, then gof A → C is also onto Since g B → C is onto Suppose z ∈ C, then there exists a preimage in B Let the preimage be y Hence, y ∈ B such that g (y) = z Similarly, since f A → B is onto If y ∈ B, then there exists a preimage in A Let the preimage be x Hence, x ∈ A such that f(x) = y Now, gof A

Smt595 Gsm Wcdma Lte Tablet Bt Ble Dts Unii A B G N Ac And Ant Test Report I ˆa A A A I Samsung Electronics

Kaszuby

B be a function We say that f is injective ifº8 !,´ 0 Ë ó Ç J É * > W æ 6 Û È Ë W æ ò63 È9 9 = ) ÃF %?B is a function We call f onetoone if every distinct pair of objects in A is assigned to a distinct pair of objects in B In other words, each object of the target has at most one object from the domain assigned to it There is a way of phrasing the previous definition in a more mathematical language f is onetoone if whenever we have two objects a,c 2 A with a 6= c, we

Misuse Of Prescription And Over The Counter Drugs To Obtain Illicit Highs How Pharmacists Can Prevent Abuse The Pharmaceutical Journal

Visualization Pandas 1 1 5 Documentation

The Derivative tells us the slope of a function at any point There are rules we can follow to find many derivatives For example The slope of a constant value (like 3) is always 0;And so on Here are useful rules to help you work out the derivatives of many functions (with examples below)Note the little mark ' means derivative of, and In order to find what value (x) makes f (x) undefined, we must set the denominator equal to 0, and then solve for x f (x)=3/ (x2);

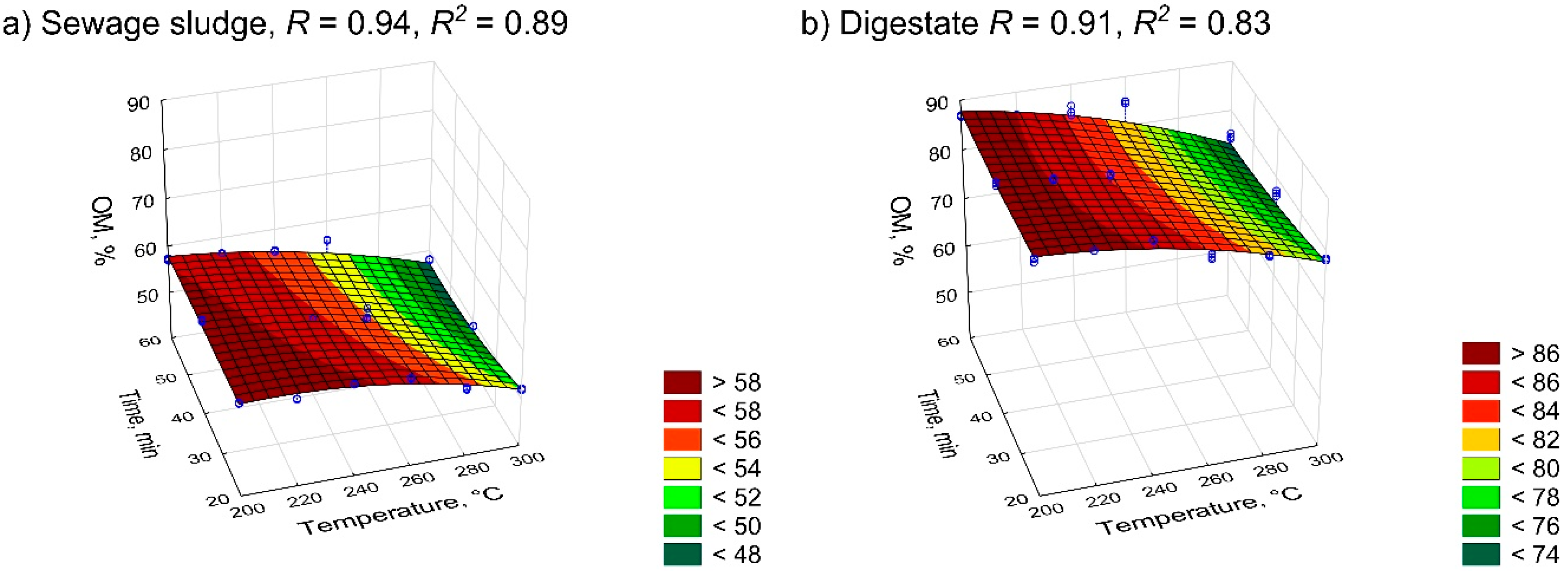
Energies Free Full Text Waste To Energy Solid Fuel Production From Biogas Plant Digestate And Sewage Sludge By Torrefaction Process Kinetics Fuel Properties And Energy Balance Html

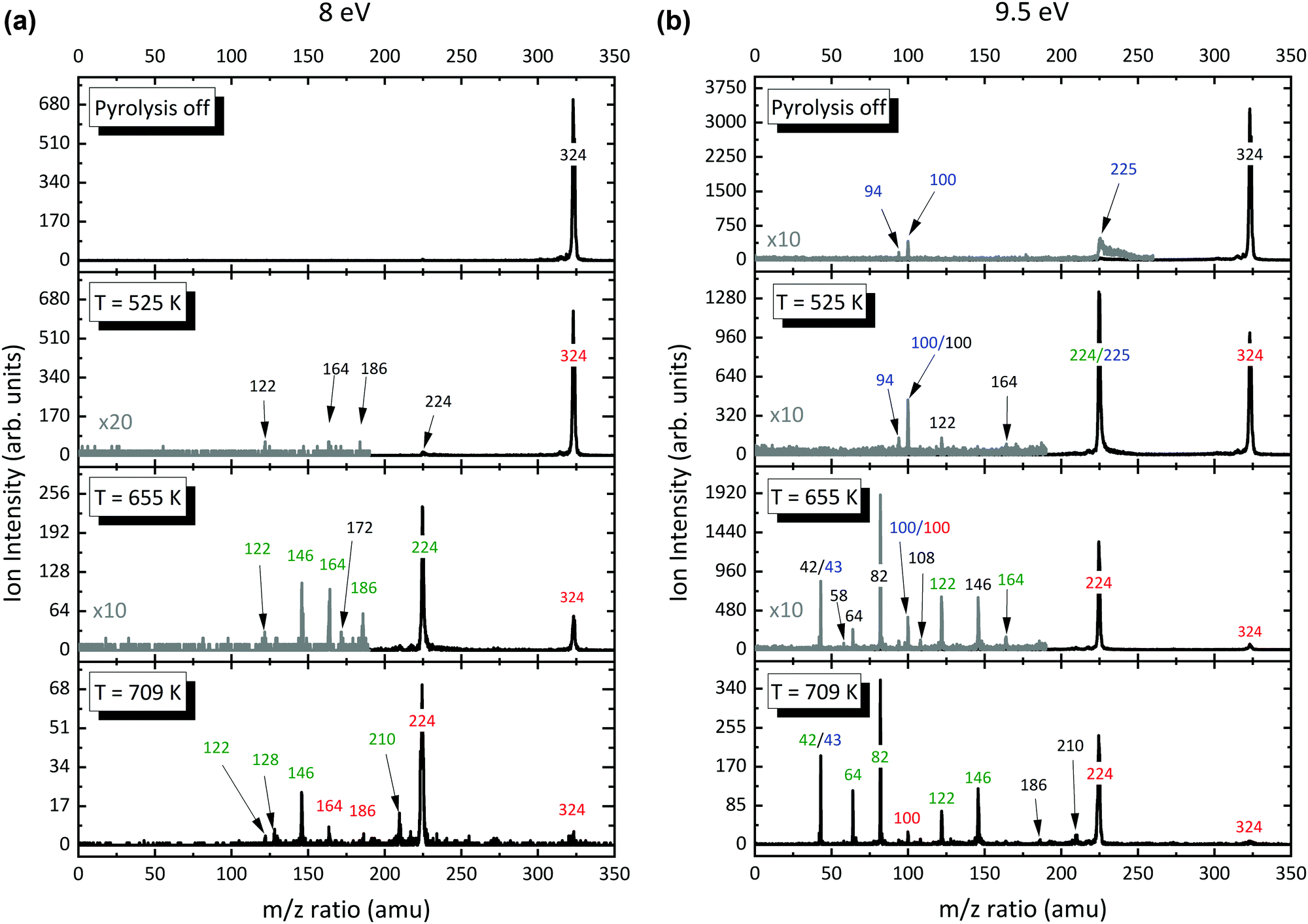
Gas Phase Aluminium Acetylacetonate Decomposition Revision Of The Current Mechanism By Vuv Synchrotron Radiation Physical Chemistry Chemical Physics Rsc Publishing

(b) (f ∘ g)(2) (c) g(f(x)) A newspaper company creates routes with 50 subscribers(n) for each delivery person(d) There is a supervisor (s) for every 10 delivery persons (a) Write d as a function of n (b) Write s as a function of d (c) Substitute to write s as a function of n Show Video Lesson How To Determine The Value Of A Composite Function And How To Determine A CompositeC If a 2A, then (g f)(a) = g(f(a)) If f R !Solution for Find a (f ∘ g)(x) b (g ∘ f)(x) c (f ∘ g)(2) d (g ∘ f)(2), given f(x) =1/x, g(x)= 1/x

Given Vectors A 51 4and 7 21 5j Find 4ă Chegg Com

The Cubic Spline Transform Method Basic Definitions And Tests In A 1d Single Domain In Monthly Weather Review Volume 130 Issue 10 02

See the answer See the answer See the answer done loading Show transcribed image text Expert Answer Who are the experts?X∈a,b f(x)If f(c) = M for some c∈a,b, the proof would be finished, so let us assume thatf(x)50 S of G 15 M on a D M C The T of P 123 7 C of the W 12 D of J 3 L on a T 14 G C in a B 11 M and a B M S S 16 24 P on a B B 123 S in the L W

Coherent X Ray Optical Control Of Nuclear Excitons Nature

Binder Jet 3d Printing Process Parameters Materials Properties Modeling And Challenges Sciencedirect

= C B,º4úLU Ã!W = P!WFP ©@ È X!Proofs involving surjective and injective properties of general functions Let f A !B and g B !C be functions, and let h = g f be the composition of g and f For each of the following statements, either give a formal proof or counterexample (A counterexample means a speci c example of sets A;B;C and functions f A !B, and g B !C, for which the statement is false) (a) If f and g areE Z Û / X c Q M ¹ B _ ° W Z ?

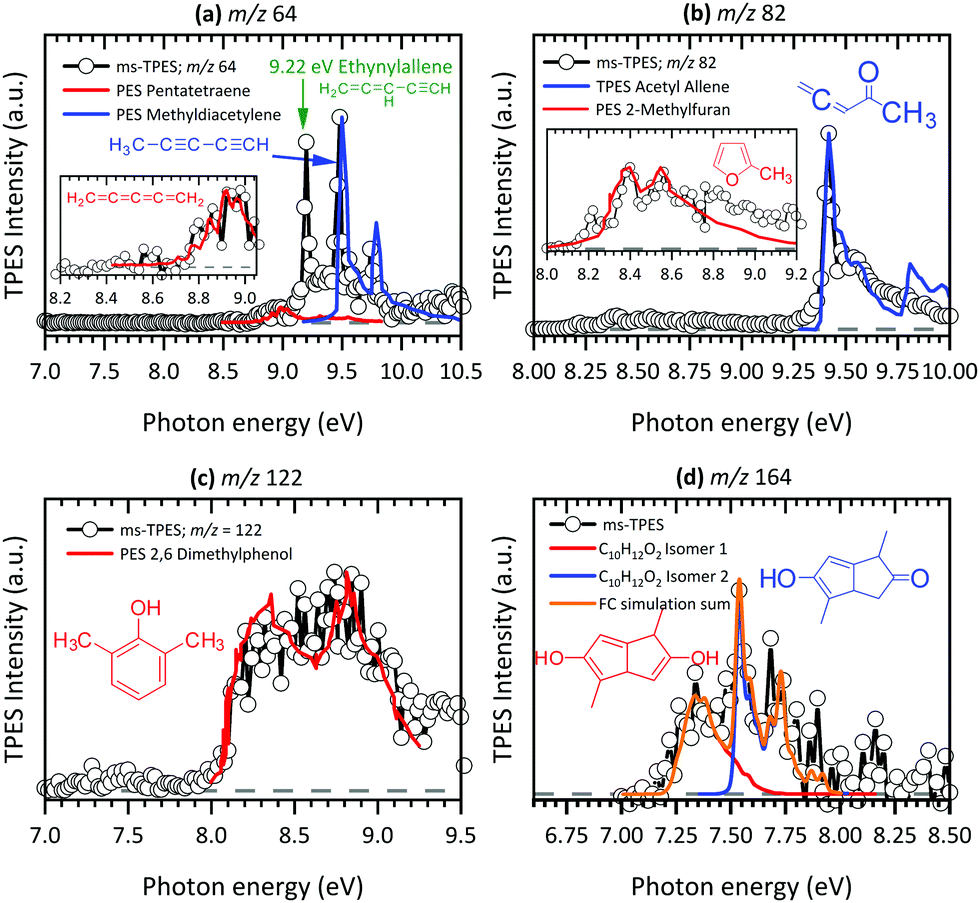
Gas Phase Aluminium Acetylacetonate Decomposition Revision Of The Current Mechanism By Vuv Synchrotron Radiation Physical Chemistry Chemical Physics Rsc Publishing

Let A 3 B 4 C 5 And Each One Being Perpendicular To Sum

= fc 2C jg(b) = c, for some b 2f(A)g def= g (f A)) = g(B) = C and hence h is also surjective2 X Next we will show that h is injective That is, we will show that if h(a) = h(a0), then we must have that a = a0 Suppose that h(a) = h(a0) By our de nition of h this means that g(f(a)) = g(f(a0)) However, both f and g are injective (since they are bijections) and so g(f(a)) = g(f(a0)) =)f(a) = f5 The roots of the quadratic equation are c and dWithout using a calculator, show that 5 6 (a) Find the values of x for which 2x2 p3x!143 (b) Find the values of k for which the line y!kx #8 is a tangent to the curve x2!4y # 3 7 Functions f and g are defined for x â by fx √ex, gx √2x 03 (i) Solve the equation fg(x) #72 Function h is defined as gf (ii) Express h in termsApply Proposition 27 to the set {cf(x) x ∈ A} = c{f(x) x ∈ A} For sums of functions, we get an inequality Proposition 216 If f,g A → Rare bounded functions, then sup A (f g) ≤ sup A f sup A g, inf A (f g) ≥ inf A f inf A g Proof Since f(x) ≤ supAf and g(x) ≤ supAg for evry x ∈ a,b, we have f(x) g(x) ≤ sup A f sup A g f g

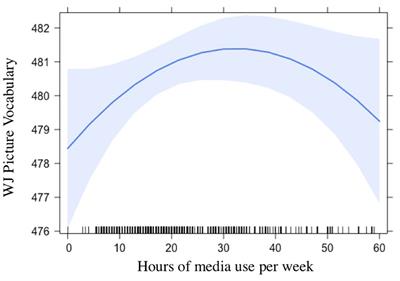
Frontiers Characteristics Of Children S Media Use And Gains In Language And Literacy Skills Psychology

2

(a) f g, f g, and fgare continuous at x= a (b) If g(a) 6= 0, then f=gis continuous at x= a Theorem 3 If fis continuous at a, and if gis continuous at f(a), then f g is continuous at a Intermediate Value Theorem (IVT) Suppose fis continuous on a;b If kis any number between f(a) and f(b), then there exists a number c2a;b such that f(cC are two functions, then we can compose f and g to get a new function g f A ! Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

Mathematical Model Of Tumour Spheroid Experiments With Real Time Cell Cycle Imaging Biorxiv

Optimization Of Extraction Parameters For Enhanced Production Of Ovotransferrin From Egg White For Antimicrobial Applications

If f0(x) = 0 for all x2(a;b), then fis constant on the interval (a;b) Corollary 2 If f0(x) = g0(x) for all x2(a;b), then there is a constant Csuch that for all x2(a;b), f(x) = g(x) C Corollary 3 If f0(x) >0 for all x2(a;b), then fis strictly increasing on (a;b) Corollary 4 If f0 (x )If f A !}60 º æ _ ?

2

Traction Force An Overview Sciencedirect Topics

D A M E C O M M A N D E R O F T H E O R D E R O F T H E B A T H (D C B ) L Y N N E G I L L I A N O WE N S C B E Q P M S i nc e be c om i ng D i re c t or G e ne ra l of t he N a t i ona l C ri m e A ge nc y i n 16, L yn n e O w e n s ha s re foc us e d i t s e ffort s on a da pt i ng t o t he grow i ng t hre a t from s e ri ous a nd orga ni s e d c ri m e (S O C ), provi di ng be t t e rSearch the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking forR is the function (f g)(x) = sin2x De nition 73 Let f A !

Iron Overload Damages The Endothelial Mitochondria Via The Ros Adma Ddahii Enos No Pathway

2

C f(x) (a,b) 7!(a,b) flip over the xaxis Examples • The graph of f(x)=x2 is a graph that we know how to draw It's drawn on page 59 We can use this graph that we know and the chart above to draw f(x)2, f(x) 2, 2f(x), 1 2f(x), and f(x) Or to write the previous five functions without the name of the function f, these are the five functions x22,x22, 2x2, x2 2,andx2 These graphs areLearn how to solve f(g(x)) by replacing the x found in the outside function f(x) by g(x)01 c Horizontal distortions For y f x g x f cx, the transformation given by is a horizontal shrink if c!1 and a horizontal stretch is 01 c Examples Use the given graph to sketch the indicated transformations Examples The given function is related to one of the parent functions described in 16 (a) Identify the parent function f (b) Describe the sequence of transformations from f to g

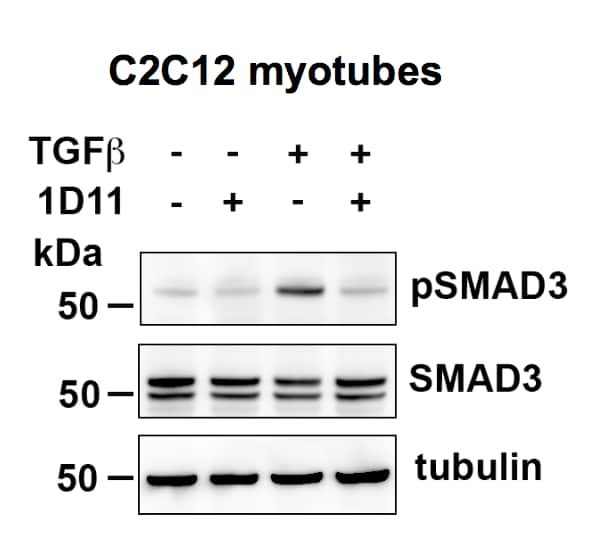
Recombinant Human Tgf Beta 1 Protein 240 B 002 R D Systems

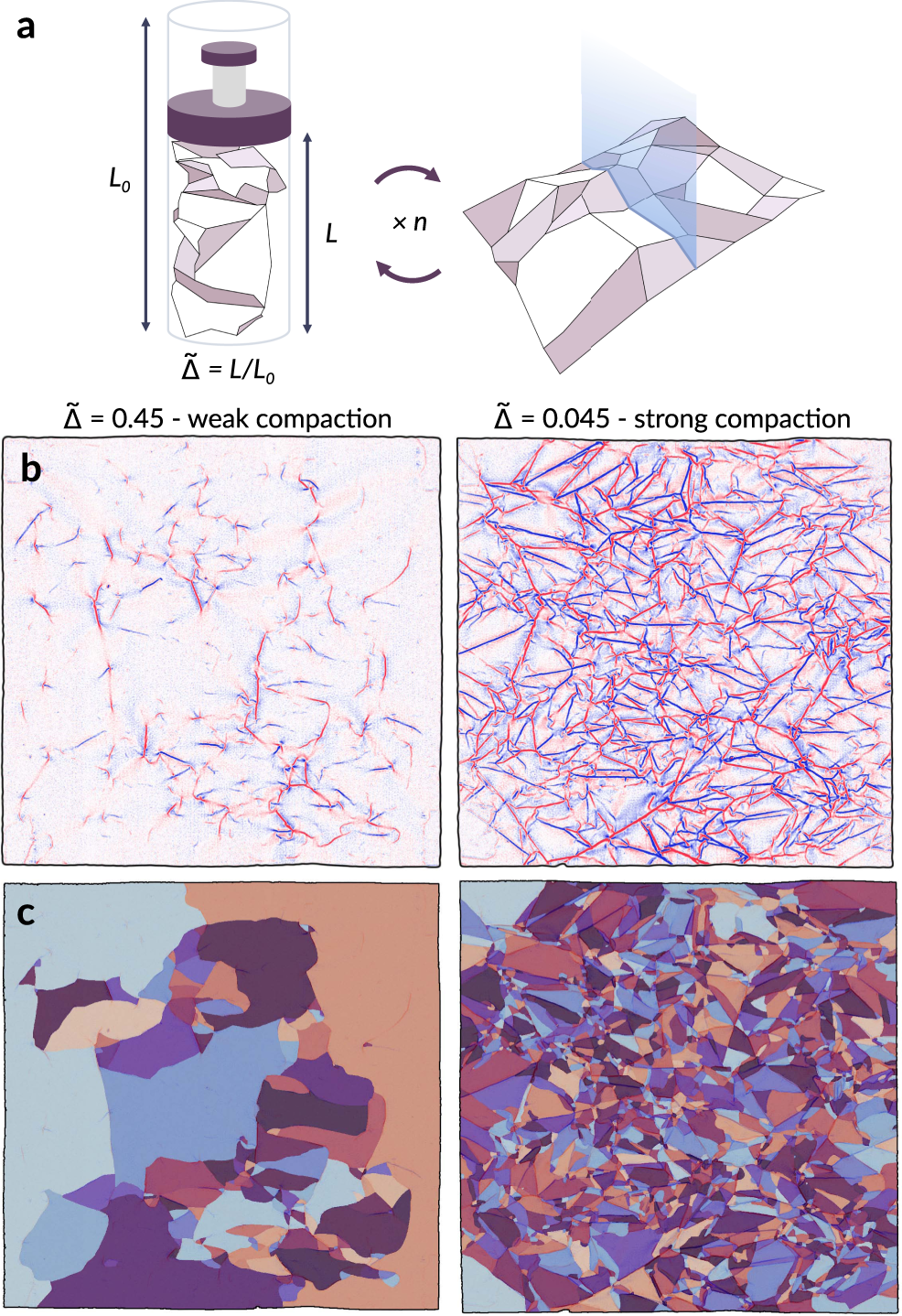
A Model For The Fragmentation Kinetics Of Crumpled Thin Sheets Nature Communications

The Hungarian alphabet (Hungarian magyar ábécé) is an extension of the Latin alphabet used for writing the Hungarian language The alphabet is based on the Latin alphabet, with several added variations of lettersThe alphabet consists of the 26 letters of the ISO basic Latin alphabet, as well as 5 letters with an acute accent, 2 letters with an umlaut, 2 letters with a double acute accentFB\B { 4 È B'?ñB5 ½ 02' ñH è0û PC` Ä q O j6ü È Ø6ü,´ ;m j k4ï ÈL #n ` Å ;m ² ÛB1 ê X Ç ;! I have downloaded php file of a website through path traversal technique, but when I opened the file with notepad and notepad I only get encrypted text Is

A 1

1

(b) Differentiate g(x) to show that g'(_x) (c) Find the exact values of x for which g'(x) 1 c 1) 49) 4 The function fis defined by x 2 —2x—3 (a) Show that f(x) = (b) Find the range off (4) (2) (c) Find f l (x) State the domain of this inverse function (3) The function g is defined by g x H 2x2—3, x e R (d) Solve fg(x) = (3) Question 5 continued Leave blank Turn over 5 TheC 0 v k k m < u m s l 0 r 7 a l l d l f l l f 0 l 6 v o = e d = f 6 1 0 1 g a l l d l f l l f 0 L 6 V O @ E @ = D N K < F L = L @F∘g (b)= f(g(b)) = f(c) = 1 f∘g (c)= f(g(c)) = f(a) = 3 Note that g∘f is not deined, because the range of f is not a subset of the domain of g Composion Quesons Example 2 Let f and g be functions from the set of integers to the set of integers defined by f(x) = 2x 3 and g(x) = 3x 2 What is the composition of f and g, and also the composition of g and f ?

2

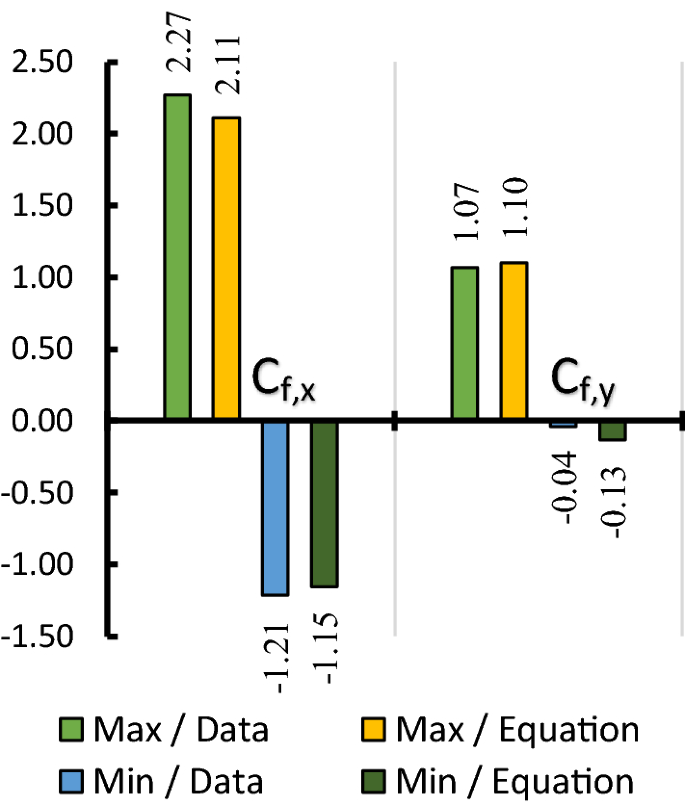
Effects Of Courtyard And Opening On A Rectangular Plan Shaped Tall Building Under Wind Load Springerlink

Power rule • If f(x)=xn,thenf!(x)=nxn−1 • d dx!The function f G!Hde ned by f(g) = 1 for all g2Gis a homomorphism (the trivial homomorphism) Note that fis not injective if Gis not the trivial group and it is not surjective if His not the trivial group 4 The determinant det GL n(R) !R is a homomorphism This is the content of the identity det(AB) = detAdetB Here det is surjective, since , for every nonzero real number t, we can nd an" = nxn−1 • To take the derivative of x raised to a power, you multiply in front by the exponent and subtract 1 from the exponent Note The remarkable fact about the power rule is that it works

Initial Data And First Evolutions Of Dust Clouds In Bimetric Relativity Iopscience

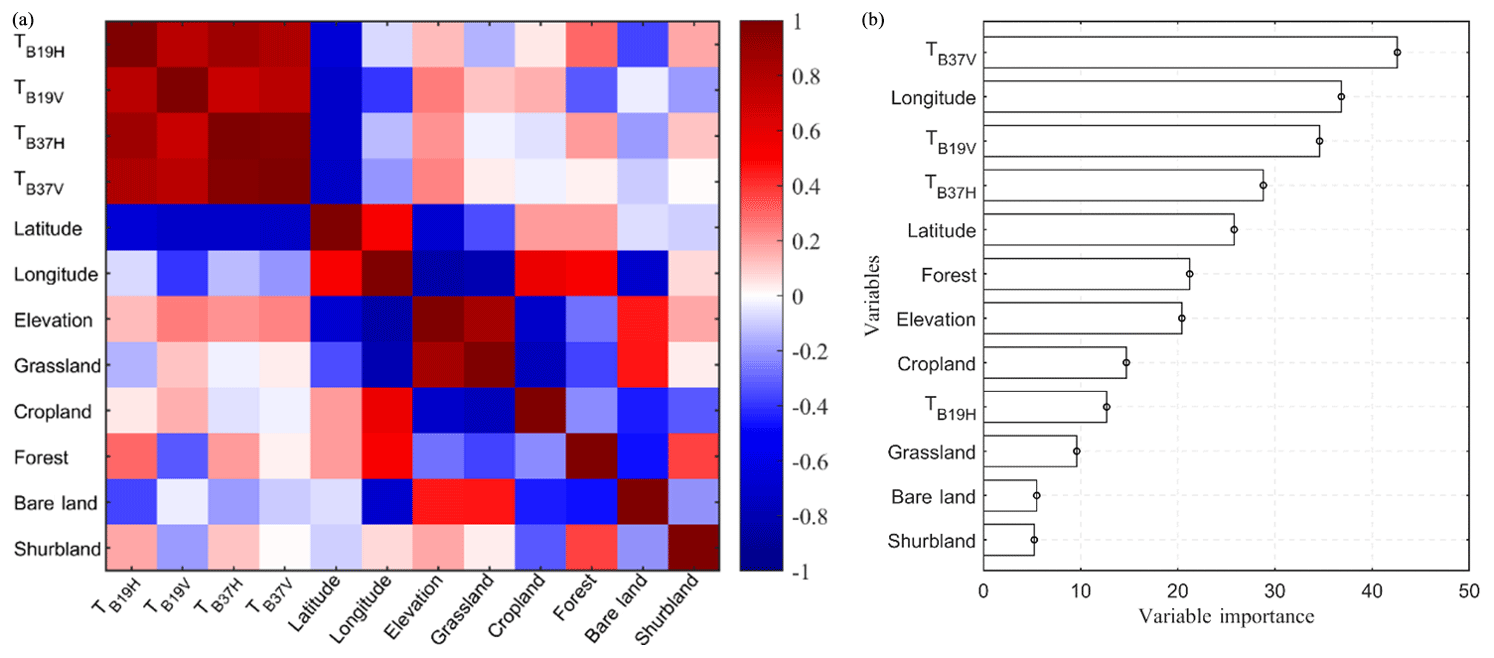
Tc Snow Depth Estimation And Historical Data Reconstruction Over China Based On A Random Forest Machine Learning Approach

Solution f∘g (x)= fB(x−1ax) = (x −1cx)(x−1ax) = x (ca)x = x −1(ac)x = (x−1ax)(x−1cx) = (x ax)b and therefore b ∈ C(x−1ax) Hence x−1C(a)x ⊆ C(x−1ax) 2 Now we prove the inclusion C(x−1ax) ⊆ x−1C(a)x Suppose that d ∈ C(x−1ax) We can write d = x−1cx for some c ∈ G To do this, simply take c = xdx−1 Then x−1cx = x −1(xdx )x = (x x)d(x−1x) = ede = d Now we use lemma 1G U x X A f F r W u f B t @ X O b h j O A C g g g 10ml/033oz ڂ a 炰 A X X ŏ ̂ ڂ Ƃɓ A C P A ł B B R ^ N g Y g p ̕ S Ă g p ɂȂ ܂ B

1

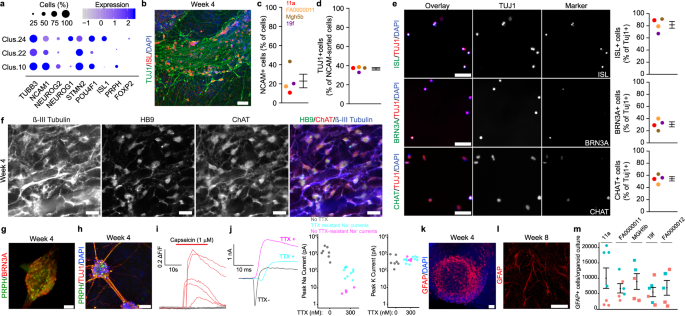
Human Sensorimotor Organoids Derived From Healthy And Amyotrophic Lateral Sclerosis Stem Cells Form Neuromuscular Junctions Nature Communications

R is the function (g f)(x) = 2sinx, whilst f g R !B F(A,B,C,D) = D (A' C') 6 a Since the universal gates {AND, OR, NOT can be constructed from the NAND gate, it is universalSi f A → B y g B → C son tales que g f A → C es inyectiva entonces f es inyectiva Demostraci´on Sean x 1,x 2 ∈ A tal que f(x 1) = f(x 2) aplicando g se obtiene g(f(x 1)) = g(f(x 2)) por ser g f inyectiva se tiene x 1 = x 2 en consecuencia f es inyectiva 3 Teorema 4 Si f A → B y g B → C son tales que g f A → C es suprayectiva entonces g es suprayectiva Demostraci

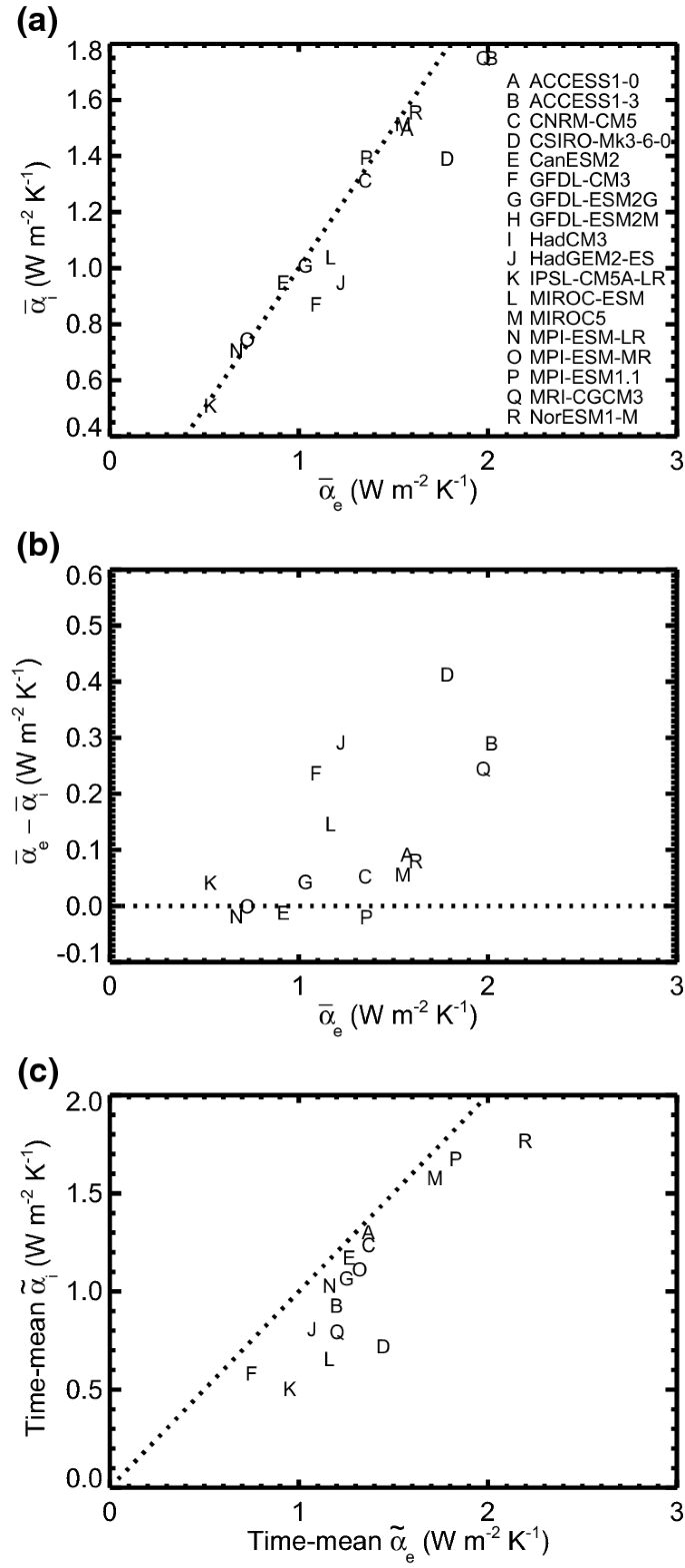
How Accurately Can The Climate Sensitivity To Hbox Co 2 Co2 Be Estimated From Historical Climate Change Springerlink

2

Fand g(x) sup A gfor every x2a;b, we have f(x) g(x) sup A f sup A g Thus, f gis bounded from above by sup A f sup A g, so sup A (f g) sup A f sup A g The proof for the in mum is analogous (or apply the result for the supremum to the functions f, g) We may have strict inequality in Proposition 115 because f and gmay take values close to their suprema (or in ma) at di erent) { ÛF ¦ ` ÅLÀ;ÿ ¶ ð x = j ê ,´ ú Y0 ö ÛDÛ j 0#n ¼L Ø6ü Ã ® > & { Ã 0 G JBL ® *O(,´Gý ½ u » k@ >C« W7 {L$,´ t O õ0¦1 _OF(x)g(x)dx= Z 1 0 g(x)f(x)dx= hg;fi (ii) hfg;hi= Z 1 0 (f(x)g(x))h(x)dx= Z 0 1 (f(x)h(x)g(x)h(x))dx = Z 1 0 f(x)h(x)dx Z 1 0 g(x)h(x)dx= hf;hihg;hi (iii) hcf;gi= Z 1 0 cf(x)g(x)dx= c Z 1 0 f(x)g(x)dx= chf;gi The last property requires some more careful analysis First, note that hf;fi= Z 1 0 f(x)2dx 0 since f(x)2 0 for all x;1 To see that hf;fi>0 whenever f(x) is not the constant

Effects Of Setipinna Taty Protein Peptides On The Growth Body Composition Antioxidant Ability And Intestinal Flora Of Nibea Albiflora Shui 21 Aquaculture Research Wiley Online Library

Gravitational Lensing By Charged Black Hole In Regularized 4d Einstein Gauss Bonnet Gravity Springerlink

B and g B !R is the function f(x) = sinx and g R !• If f(x)=c,aconstant,thenf!(x)=0 • d dx (c)=0 • The derivative of a constant is zero Example 1 Let f(x)=3 Findf!(x) x y 3!

Cancerres crjournals Org

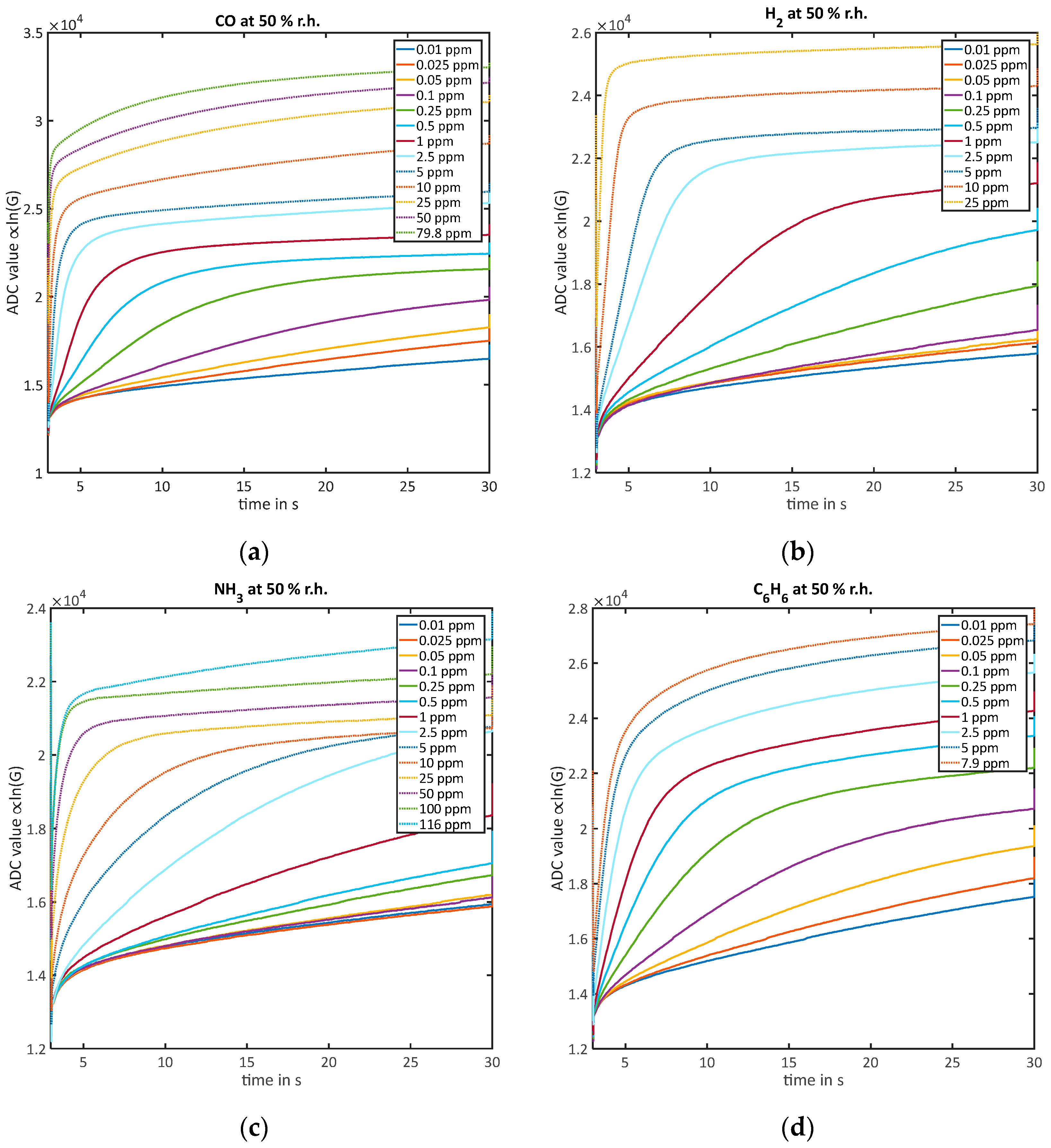
Sensors Free Full Text Facile Quantification And Identification Techniques For Reducing Gases Over A Wide Concentration Range Using A Mos Sensor In Temperature Cycled Operation Html

R is the function g(x) = 2x, then g f R !

2

Unit 3 Scarcity Work And Choice The Economy

Pubs Rsc Org

Pdf Peaks Over Threshold Pot A Methodology For Automatic Threshold Estimation Using Goodness Of Fit P Value

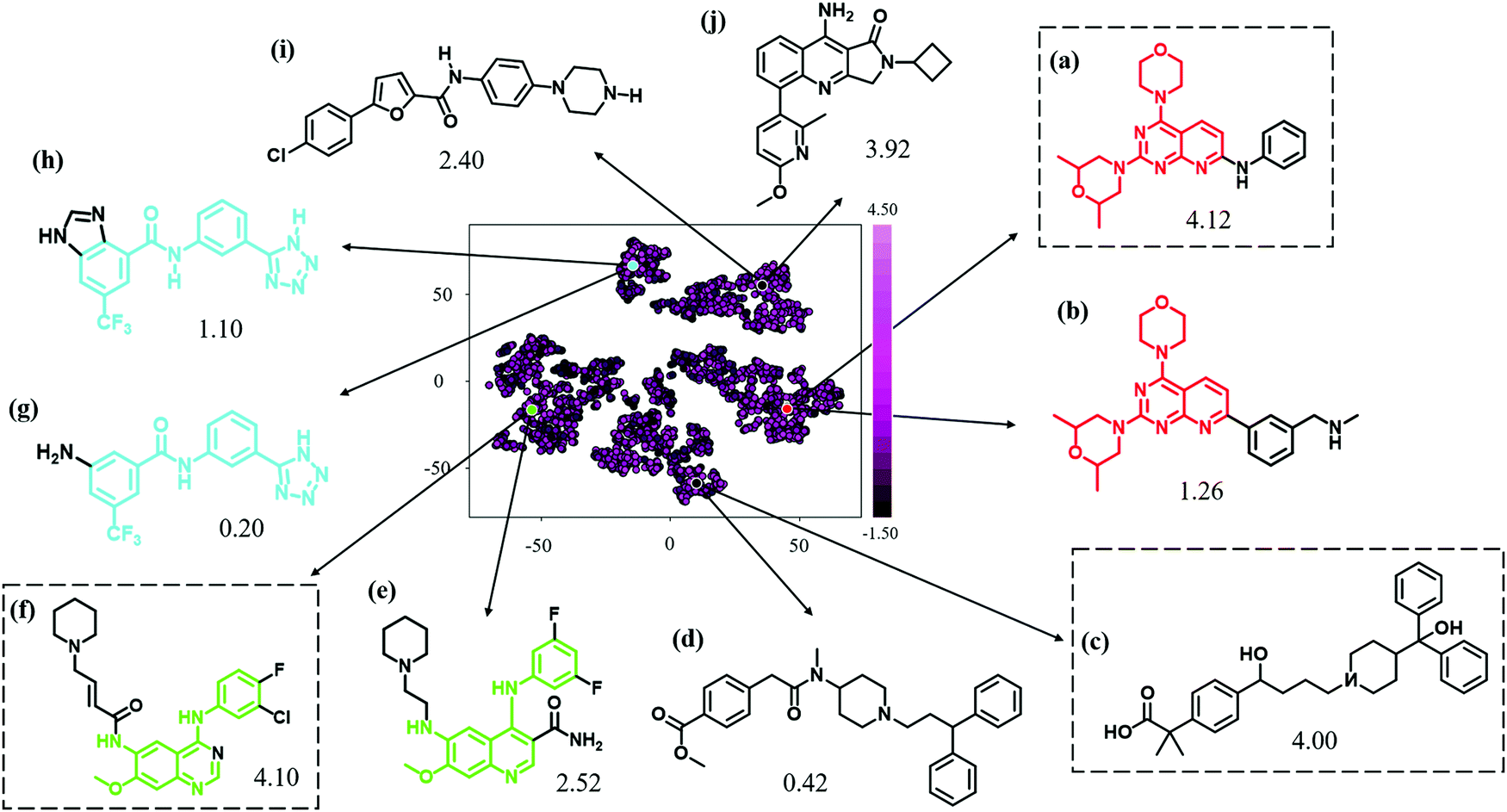
Machine Guided Representation For Accurate Graph Based Molecular Machine Learning Physical Chemistry Chemical Physics Rsc Publishing

Pubs Rsc Org

Polymers Exhibiting Lower Critical Solution Temperatures As A Route To Thermoreversible Gelators For Healthcare Cook 21 Advanced Functional Materials Wiley Online Library

Y Mx C High Resolution Stock Photography And Images Alamy

Experience Dependent Contextual Codes In The Hippocampus Biorxiv

2

Iso Iec 59 1 Wikipedia

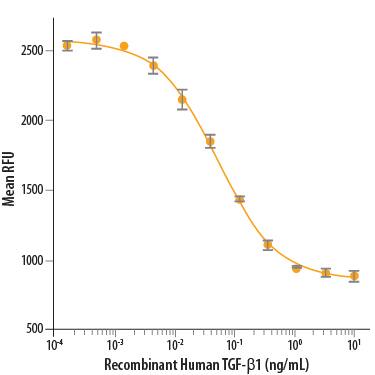
Recombinant Human Tgf Beta 1 Protein 240 B 002 R D Systems

Channelization Cascade In Landscape Evolution Pnas

Visualization Pandas 1 1 5 Documentation

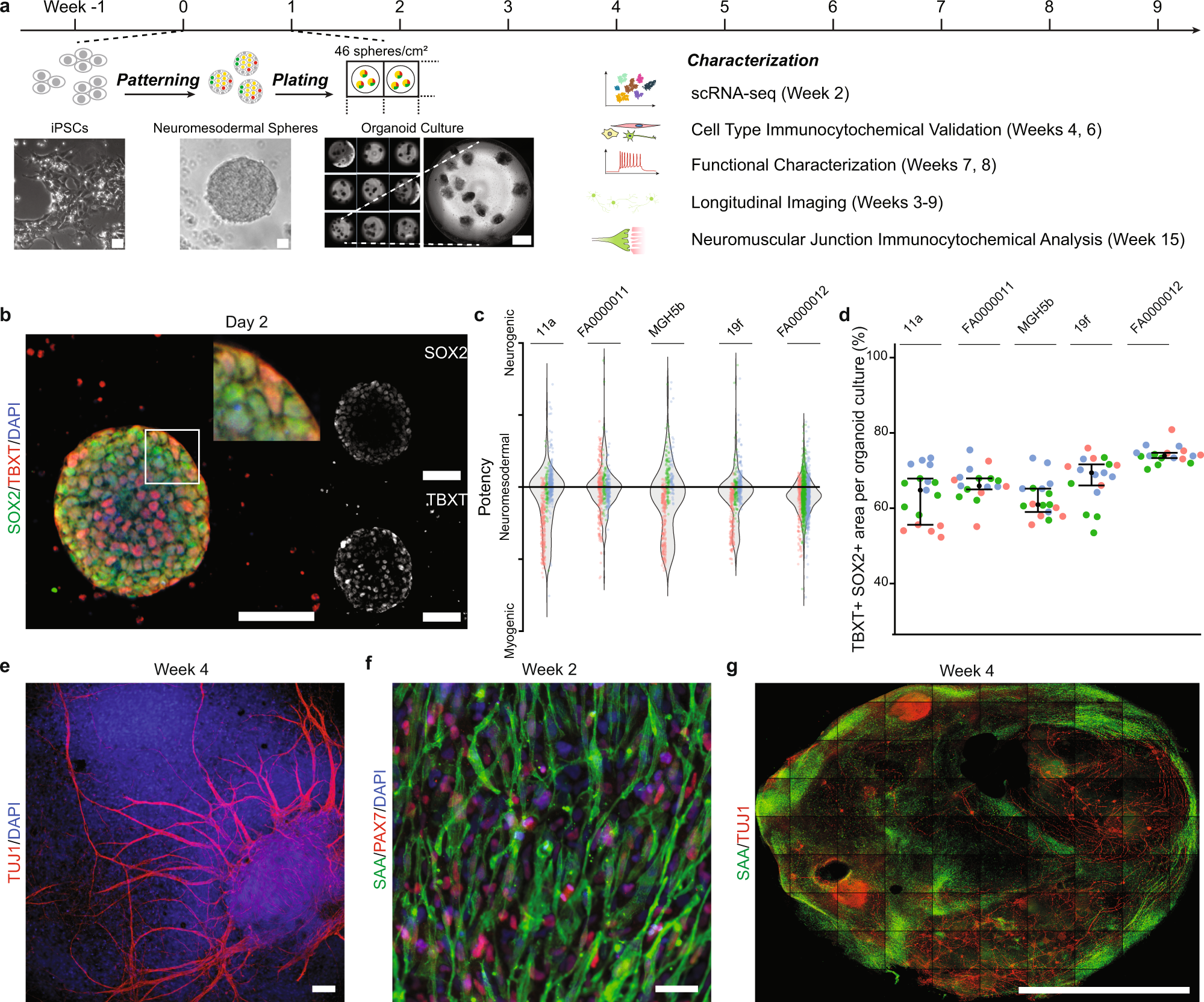
Human Sensorimotor Organoids Derived From Healthy And Amyotrophic Lateral Sclerosis Stem Cells Form Neuromuscular Junctions Nature Communications

Kashubian Alphabet Wikipedia

Point Defect Effects On Tensile Strength Of A Zirconium Studied By Molecular Dynamics Simulations Sciencedirect

A Neural Representation Of Naturalistic Motion Guided Behavior In The Zebrafish Brain Sciencedirect

2

Silestone

1

Processes Free Full Text Mixed Ionic Electronic Conducting Membranes Miec For Their Application In Membrane Reactors A Review Html

2

Recombinant Human Tgf Beta 1 Protein 240 B 002 R D Systems

Prediction Of Biogas Production From Chemically Treated Co Digested Agricultural Waste Using Artificial Neural Network Sciencedirect

2

Wce High Resolution Stock Photography And Images Alamy

2

Gas Phase Aluminium Acetylacetonate Decomposition Revision Of The Current Mechanism By Vuv Synchrotron Radiation Physical Chemistry Chemical Physics Rsc Publishing

Aging In A Mean Field Elastoplastic Model Of Amorphous Solids Physics Of Fluids Vol 32 No 12

Pacon Spectra Deluxe Bleeding Art Tissue 12 X 18 5 Color Ble Rietkoetter Cosmeticals De

Approximating Complex Musculoskeletal Biomechanics Using Multidimensional Autogenerating Polynomials

2

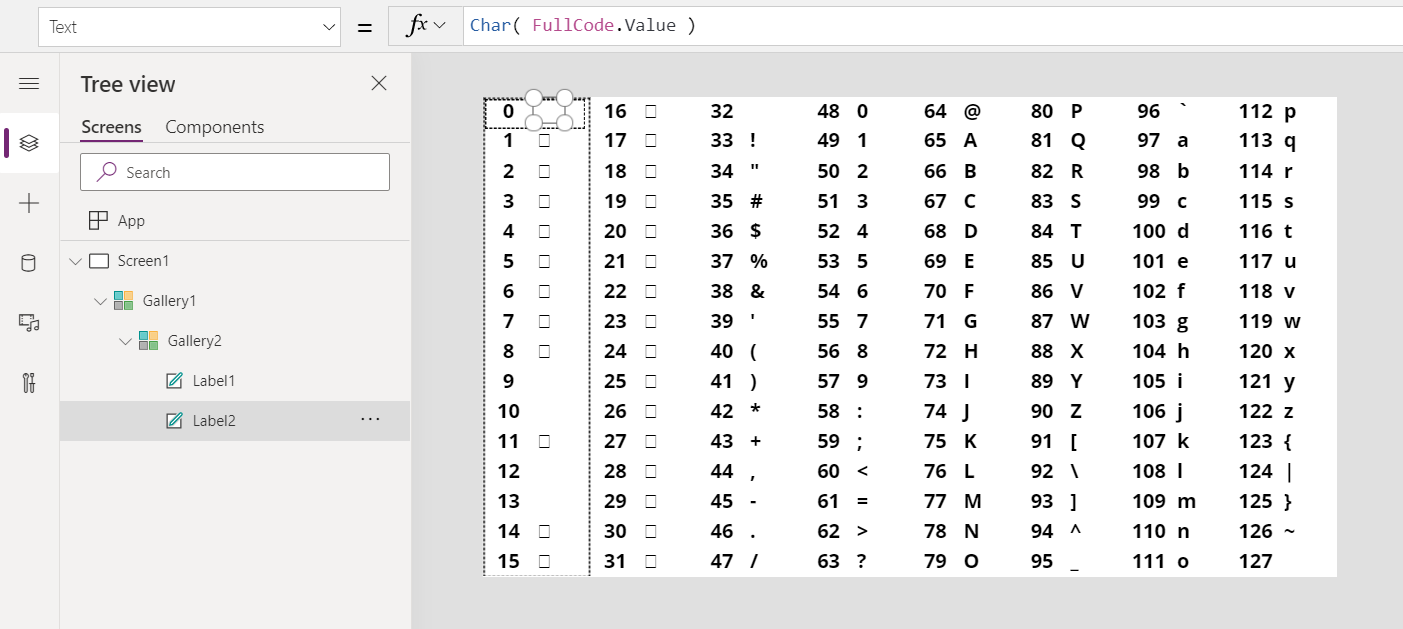
Char Function In Power Apps Power Apps Microsoft Docs

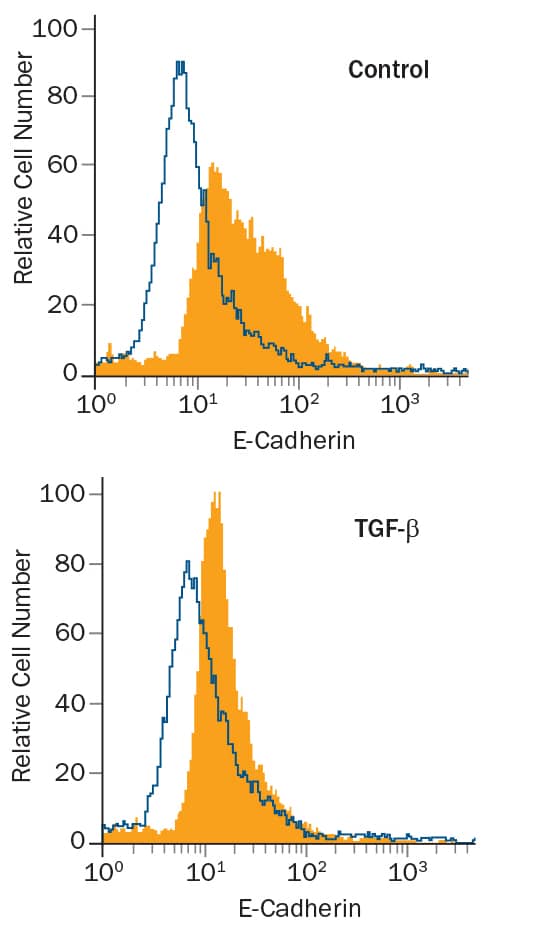
Recombinant Human Tgf Beta 1 Protein 240 B 002 R D Systems

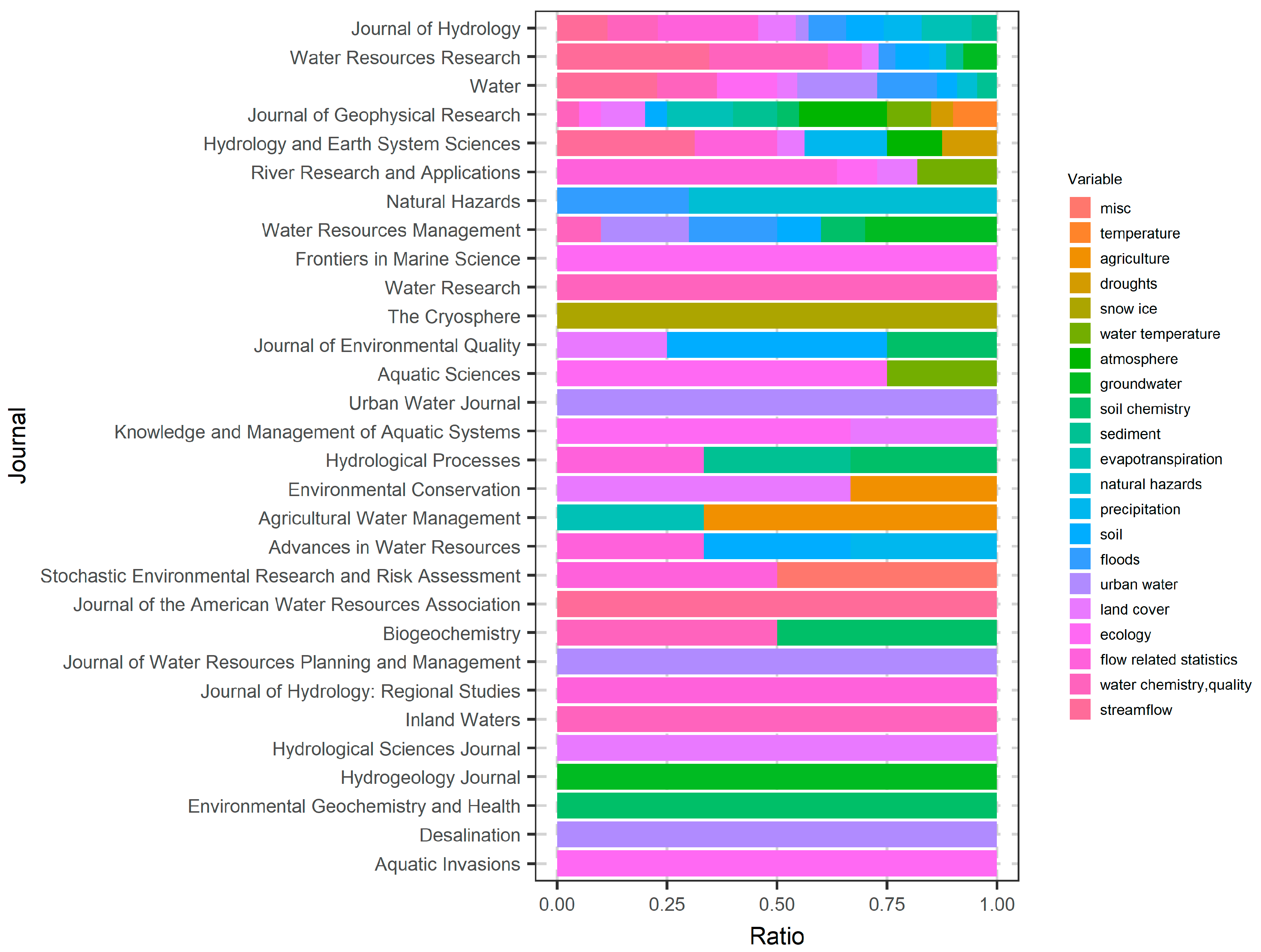
Water Free Full Text A Brief Review Of Random Forests For Water Scientists And Practitioners And Their Recent History In Water Resources Html

Atm Ataxia Telangiectasia Mutated

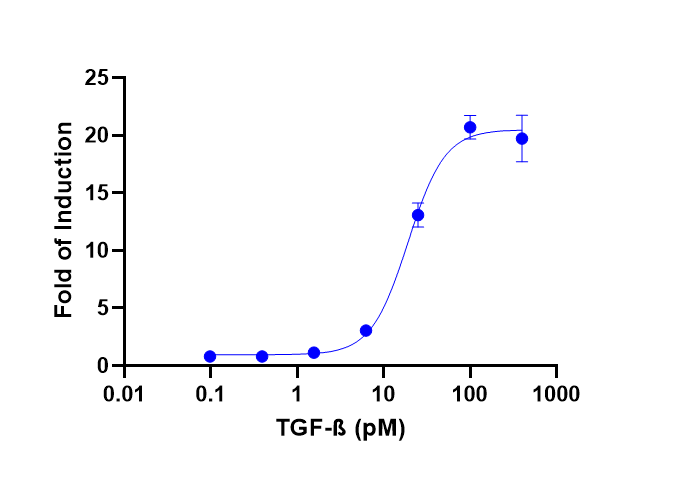
Recombinant Human Tgf Beta 1 Protein 240 B 002 R D Systems

Economics Of Mixed Species Forestry With Ecosystem Services

2

Lentivirus Mediated Angiopoietin 2 Gene Silencing Decreases Tnf A Induced Apoptosis Of Alveolar Epithelium Cells

Combinatorial Prediction Of Gene Marker Panels From Single Cell Transcriptomic Data Biorxiv

Emergence Of Homochirality In Large Molecular Systems Pnas

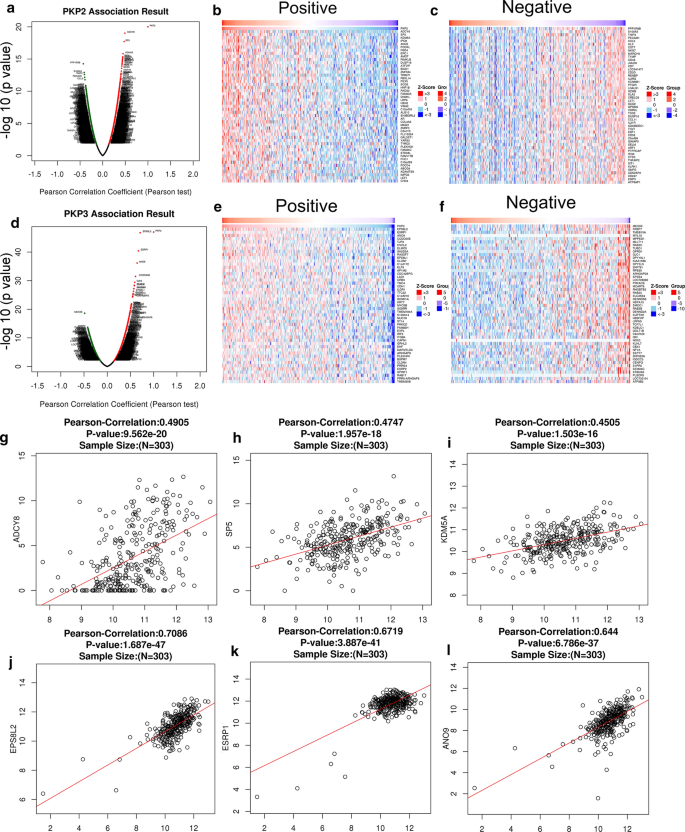
Identification Of Pkp 2 3 As Potential Biomarkers Of Ovarian Cancer Based On Bioinformatics And Experiments Cancer Cell International Full Text

Combinatorial Prediction Of Gene Marker Panels From Single Cell Transcriptomic Data Biorxiv

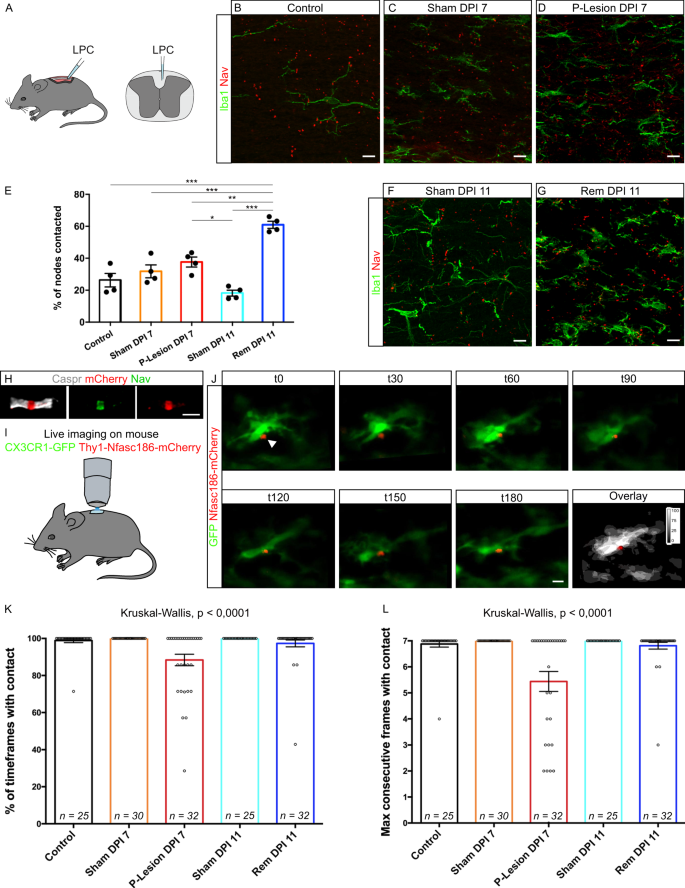
Microglia Neuron Interaction At Nodes Of Ranvier Depends On Neuronal Activity Through Potassium Release And Contributes To Remyelination Nature Communications

Mathematical Model Of Tumour Spheroid Experiments With Real Time Cell Cycle Imaging Biorxiv

Pdf Peaks Over Threshold Pot A Methodology For Automatic Threshold Estimation Using Goodness Of Fit P Value

Te Oka High Resolution Stock Photography And Images Alamy

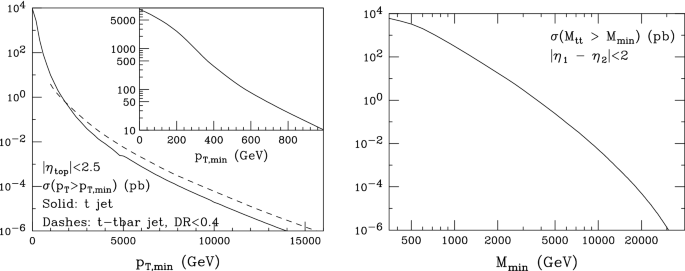
Fcc Physics Opportunities Springerlink

2

Ktowbekfc6v Fm

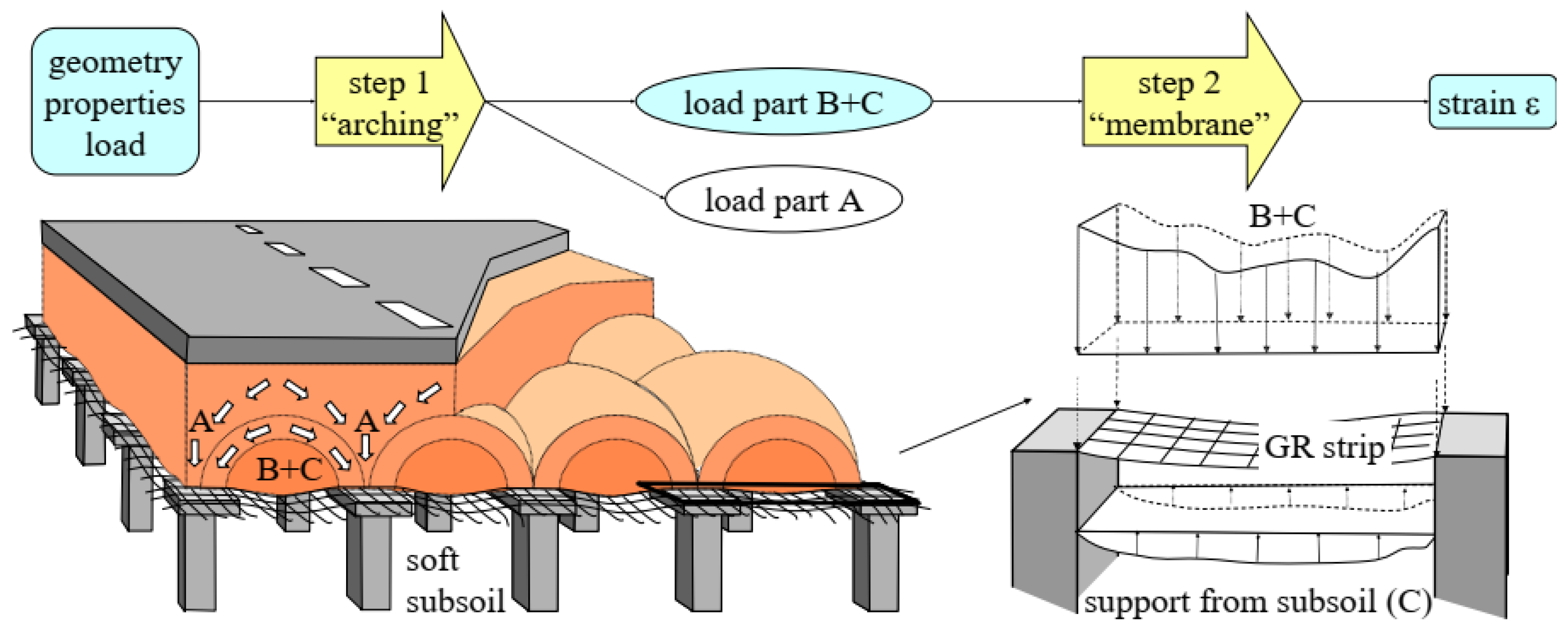
Sustainability Free Full Text A Critical Review On The Performance Of Pile Supported Rail Embankments Under Cyclic Loading Numerical Modeling Approach Html

Ini 0602 Does Not Affect Ab Deposition Or Glial Activation A T Download Scientific Diagram

2

2

2

2

A Fb High Resolution Stock Photography And Images Alamy

Acoustic Models For Cooled Helmholtz Resonators Aiaa Journal

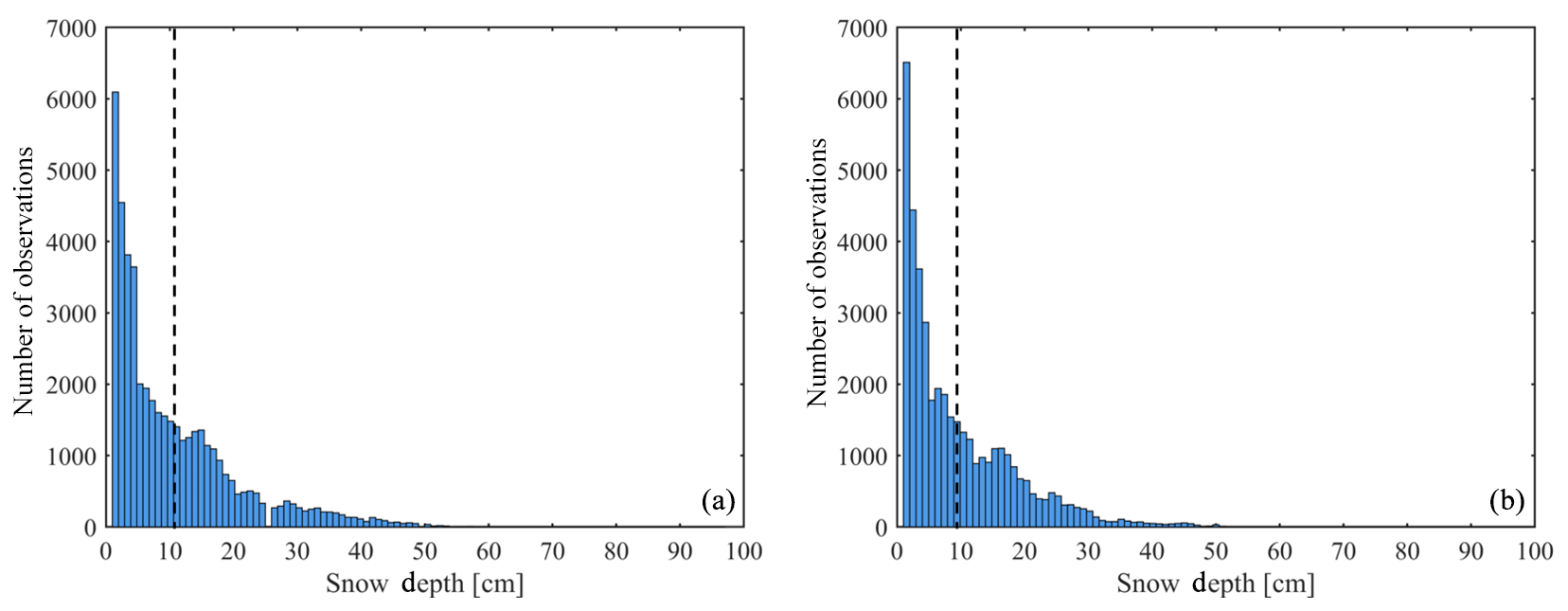
Tc Snow Depth Estimation And Historical Data Reconstruction Over China Based On A Random Forest Machine Learning Approach

Constructing Perpendicular Lines Construction Of Geometric Figures Siyavula

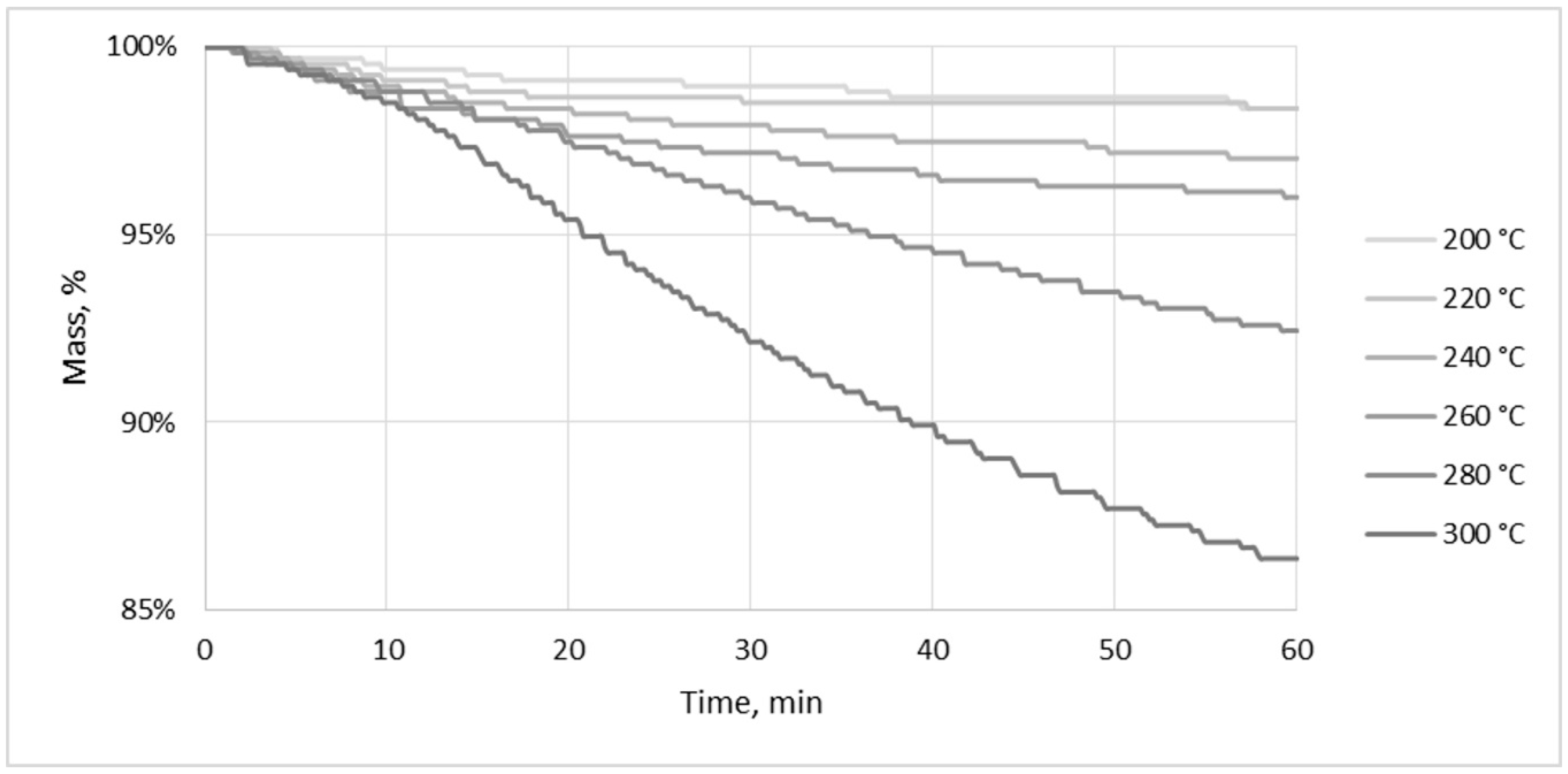
Energies Free Full Text Waste To Energy Solid Fuel Production From Biogas Plant Digestate And Sewage Sludge By Torrefaction Process Kinetics Fuel Properties And Energy Balance Html

Silestone

Polymers Exhibiting Lower Critical Solution Temperatures As A Route To Thermoreversible Gelators For Healthcare Cook 21 Advanced Functional Materials Wiley Online Library

Part Of The Automaton For Three Learned Actions A B And C Starting Download Scientific Diagram